FUNÇÃO DE SEGUNDO GRAU

 

Função do 2º grau ou função quadrática

Definimos como função do 2º grau, ou função quadrática, a função R → R, ou seja, uma função em que o domínio e o contradomínio são iguais ao conjunto dos números reais, e que possui a lei de formação f(x) = ax² +bx +c.

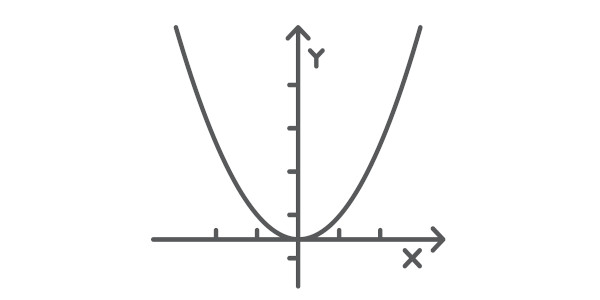
O gráfico da função quadrática é sempre uma parábola e possui elementos importantes, que são:

• as raízes da função quadrática, calculadas pelo x’ e x”;
• o vértice da parábola, que pode ser encontrado a partir de fórmulas específicas.

O que é uma função do 2º grau?

Uma função polinomial é conhecida como função do 2º grau, ou também como função quadrática, quando em sua lei de formação ela possui um polinômio de grau dois, ou seja, f(x) = ax² +bx +c, em que a, b e c são números reais, e a ≠ 0. Além da lei de formação, essa função possui domínio e contradomínio no conjunto dos números reais, ou seja, f: R→ R.

A raízes de uma função quadrática são os valores de x que fazem com que f(x) = 0. Sendo assim, para encontrar as raízes de uma equação do 2º grau, faremos ax² + bx + c = 0.

link: https://mundoeducacao.uol.com.br/matematica/funcao-2-grau.htm

Acessado em 23/11/2021 

Comentário: 

sabendo dos conceitos da função quadrática resolvendo a seguinte função f(x)= x²+4x+3  chegamos as seguintes conclusões: 

a=1, b=4, c= 3 

Δ =b² – 4ac           

Δ = 4² - 4*(1)*3

Δ = 16 -12 

Δ = 4

onde X' será:  (-4 + 2)/2=  -2/2 = -1 

e X'' será: (- 4 - 2 )/2 = -6/2= -3

Então se Δ > 0 a função possui duas raízes reais diferentes , sabemos que por a>0 a concavidade da parábola no gráfico  é pra cima.