Função bijetora

Quando dizemos que uma função é bijetora (também chamada de bijetiva ou bijeção), significa que a função é injetora  e sobrejetora  ao mesmo tempo. Vamos relembrar estes conceitos:

Função injetora e sobrejetora

Uma função f é definida como uma relação entre dois conjuntos quaisquer, A e B, e uma regra que permite associar a cada elemento de A um único elemento de B. Isto quer dizer, em linguagem matemática, que:

f : A → B

Lê-se: f de A em B.

Chamamos o conjunto A de Domínio da função e B o Contradomínio. É importante atentar-se à diferença entre função f, que é a própria função, e f(x) que é o valor da função em um determinado ponto x no seu domínio. Sendo assim, podemos dizer que para cada valor de x que pertence ao domínio A, existe um único valor y (ou f(x)) que pertença ao contradomínio B. Usualmente escrevemos:

y=f(x)↔{x∈A e y∈B}

Podemos representar uma função através de um diagrama, como no exemplo abaixo:

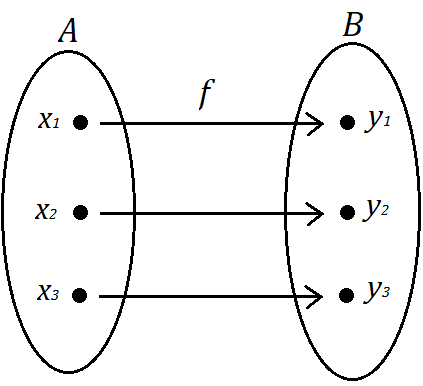
Também temos que uma função é chamada de injetora quando ela obedece estas condições:

(∀x1,x2∈A)x1≠x2⇒f(x1)≠f(x2)

Lê-se: Para quaisquer x₁, x₂ pertencentes ao conjunto A onde x₁ é diferente de x₂ então f(x₁) é diferente de f(x₂).

Uma função (ou aplicação) f : A → B é dita sobrejetora quando, para todo y∈B existe pelo menos um y∈B tal que f(x) = y. Em linguagem matemática escrevemos:

(∀y)y∈B⇒∃x∈A:f(x)=y

Lê-se: Para qualquer y, onde y pertence ao conjunto B, então existe x pertencente ao conjunto A tal que f(x) = y.

Função bijetora

Como dito anteriormente, uma função bijetora é tanto injetora quanto sobrejetora. Logo, as definições de injeção e sobrejeção valem para uma mesma função quando está é chamada de bijetora/bijetiva. Vejamos alguns exemplos:

Exemplo 1) Dada a aplicação f:R→R definida pela lei f(x)=3x+1, é bijetora, pois:

→ Dados x1,x2∈R então vale dizer que:

3x1+1≠3x2−1⇒f(x1)≠f(x2)

Então f é injetiva.

→ Dado y∈R então existe x∈R onde f(x) = y. Provando isto, temos:

3x+1=y⇒x=y−13

Note que para qualquer valor de y na igualdade acima existirá um valor real x que satisfaz a condição de sobrejeção.

Concluindo, a função f(x) = 3x+1 é bijetora.

Observação:

As funções não podem ser divididas em injetivas e sobrejetivas porque existem diversas aplicações que não são nem uma coisa nem outra. Um caso clássico é a função do tipo f:R→R definida por f(x)=x2 , onde ela não é nem sobrejetiva e nem injetiva. Veja:

2≠−2, porém f(2)=4=f(−2). Logo não é injetiva.

−1∈R , mas −1∉Im(f)=R+. Também não é sobrejetiva.

link: https://www.infoescola.com/matematica/funcao-bijetora/

acessado em 27/11/2021

comentário:  vemos que a função bijetora é quando a função é simultaneamente injetora e sobrejetora: ou seja  quando a imagem é igual ao contradomínio e ao mesmo tempo quando tiver elementos diferentes do domínio devem ter imagens diferentes.