Função raiz

A função raiz é dada por f(x) = x1/n. Nessa expressão, x é o domínio, f(x) é imagem e 1/n é o expoente.

Nessa figura, temos três funções: a raiz, a do segundo grau e a linear

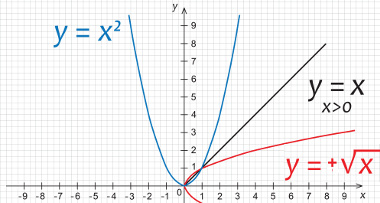
Para termos uma função, é necessário estabelecer uma relação entre dois conjuntos, que são:

• Domínio → x

• Imagem → y = f(x)

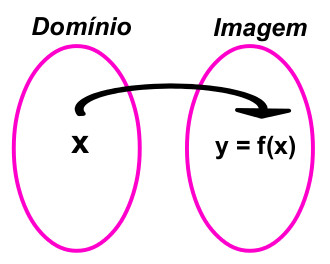
O gráfico de toda função em duas dimensões é definido no plano cartesiano, em que o eixo x é a abscissa e o eixo y é a ordenada. Veja:

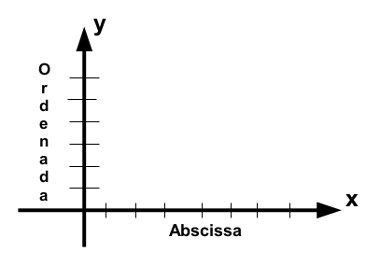
FUNÇÃO RAIZ

A função raiz é definida pela fórmula:

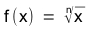
f(x) = imagem
x = domínio
n = índice

Podemos reescrever da seguinte forma:

f(x) = x1/n

• f(x) = imagem;

• 1/n = expoente. O n sempre deve ser positivo, ou seja, um número natural;

• x = domínio. O x pode ser positivo ou negativo. Para x positivo, n pode ser ímpar ou par; para x seja negativo, n poderá ser somente ímpar. Essa restrição está relacionada com o fato de não existir raiz quadrada para n par e x negativo.

GRÁFICO DA FUNÇÃO RAIZ

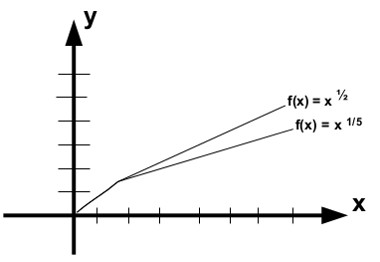
A função raiz é positiva e crescente. À medida que o valor numérico de n aumenta, o crescimento diminui. Veja um comparativo:

Para f(x) = x ½ (n = 2) e f(x) = x 1/5 (n = 5):

EXEMPLOS DE FUNÇÃO RAIZ

1) Resolva as funções. Considere x = 16.

a) f(x) = x ½

b) f(x) = x1/4

Solução

a) f(x) = x ½

f(x) = 161/2

Fatore:

16|2
08|2
04|2
02|2
01|

f(x) = (2)4 . ½

f(x) = (2)4/2

f(x) = (2)2

f(x) = 4

b) f(x) = x1/4

f(x) = 161/4

Utilize a fatoração obtida anteriormente:

f(x) = 24 . ¼

f(x) = 24/4

f(x) = 21

f(x) = 2

Link:https://mundoeducacao.uol.com.br/matematica/funcao-raiz.htm

Acessado em 27/11/2021

Comentário: sabemos que a função raiz é real e positiva para qualquer valor de X porque sabemos que  X pertence ao conjunto dos números naturais logo a função raiz exige uma fatoração e pode ser utilizada por exemplo para determinação de áreas para fins geométricos.