Função exponencial

A função exponencial é utilizada para descrever e modelar o comportamento de várias situações no nosso dia a dia. Podemos observá-la, por exemplo, na matemática financeira, em situações que envolvem juros compostos, em reprodução de cultura de bactérias, e até mesmo o comportamento de novos casos da covid-19, durante a pandemia em 2020, aproxima-se muito de um comportamento exponencial.

A lei de formação da função exponencial é f(x) = ax, podendo gerar um gráfico crescente ou decrescente, dependo do valor da base “a”. A função inversa da função exponencial é a função logarítmica.

Definição da função exponencial

Definimos como função exponencial uma função f: ℝ → ℝ*+, ou seja, seu domínio é o conjunto dos números reais, e seu contradomínio é o conjunto dos números reais positivos diferentes de 0. Além disso, a sua lei de formação pode ser descrita por f (x) = ax, em que ‘a’ é a base, cujo valor sempre será um número real positivo.

Exemplos:

f(x) = 2x

f(x) = 0,3x

Podemos observar que f(x) é a variável dependente, podendo ser representada por y também, e x é a variável independente.

Tipos de função exponencial

Podemos dividir a função exponencial em dois casos: crescente ou decrescente.

O gráfico da função f(x) = ax é crescente quando a base é um número maior do que 1, ou seja, quando a > 1. Nesse caso, quanto maior o valor de x maior será o valor de y.

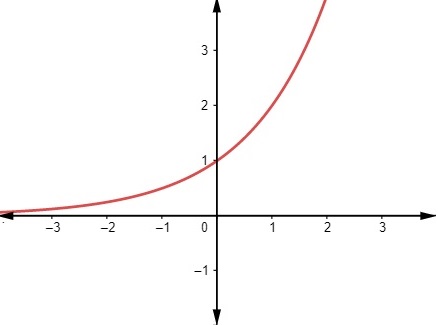
A função exponencial é decrescente quando a base é um número maior que 0 e menor que 1, ou seja, quando 0<a<1. Caso ela seja decrescente, quanto maior o valor de x menor será o valor de y.

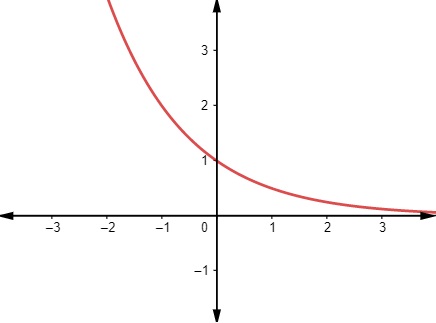
Gráfico da função exponencial

Para traçar o gráfico de uma função exponencial, é necessário encontrar o valor numérico para alguns valores de x. Existem duas possibilidades para o comportamento do gráfico, ele pode ser crescente ou decrescente, como vimos anteriormente. Quando o gráfico é crescente, a função exponencial é caracterizada por possuir um crescimento muito rápido em comparação, por exemplo, com a função afim.

Podemos observar que o gráfico não passa pelo 3º e 4º quadrante do plano cartesiano, pois o contradomínio será, como vimos na definição, os reais positivos e maiores que 0. Por mais próximo que o gráfico chegue do eixo x, ele não o tocará, não há valor algum no domínio que faça com que ax seja igual a 0, lembrando que, por definição, a base é sempre maior do que 0.

Propriedades da função exponencial

1ª propriedade

Em uma função exponencial, f(0) = 1. Essa propriedade não passa de uma consequência das propriedades de potência, já que a base de todo número diferente de 0 elevado a 0 é igual a 1.

f(0) = a0=1

2ª propriedade

A função exponencial é injetiva. Isso significa que, para valores diferentes de x, a imagem também será diferente, ou seja, f(x1) ≠ f(x2) com x1 ≠ x2. Ser injetiva significa que, para valores diferentes de y, existirá um único valor de x que faz com que f(x) seja igual a y.

3ª propriedade

Como vimos em um tópico anterior, o gráfico da função exponencial pode ser crescente, se a base for maior que 1 (a >1), e decrescente, caso a base seja um número menor que 1 e maior que 0 (0<a<1).

4ª propriedade

O gráfico da função exponencial nunca corta o eixo x. Por menor que seja o valor da imagem, ele nunca chegará a ser 0. Dizemos que ele tende a 0, mas não existe valor de x que faça com que f(x) = 0.