função ímpar

Uma função real de variável real  é ímpar se e só se verificar a condição , para todo o valor de x pertencente ao domínio de . Por outras palavras, uma função é ímpar quando a objetos simétricos correspondem imagens simétricas. Em termos geométricos, o gráfico de uma função ímpar admite uma simetria em relação à origem dos eixos coordenados.
Nota: O domínio de uma função ímpar também será simétrico em relação à origem do referencial.
São exemplos de funções ímpares as seguintes funções: 

 = sin x
 = tan x
 = x3

Acessado em 28/11/2021 

Link: https://www.infopedia.pt/$funcao-impar

Comentário: Valores de domínios opostos geram imagens opostas se x  é elevado a um expoente ímpar a função é ímpar , também vale para soma  o que significa que sua função no gráfico será simétrica e terá a mesma representação só que da forma positiva e negativa exemplo: F(x)= 3,-3  ou F(x)= 5,-5 e etc.

 

Função raiz

A função raiz é dada por f(x) = x1/n. Nessa expressão, x é o domínio, f(x) é imagem e 1/n é o expoente.

Nessa figura, temos três funções: a raiz, a do segundo grau e a linear

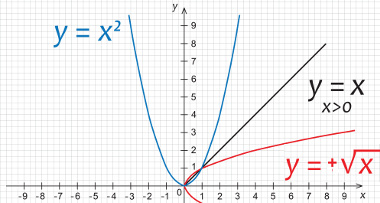
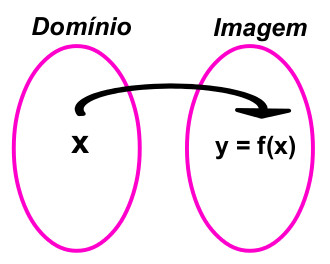
Para termos uma função, é necessário estabelecer uma relação entre dois conjuntos, que são:

• Domínio → x

• Imagem → y = f(x)

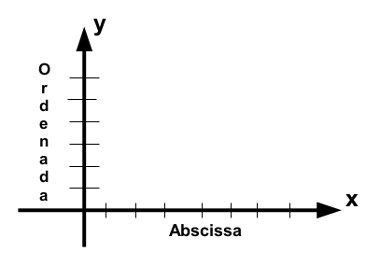
O gráfico de toda função em duas dimensões é definido no plano cartesiano, em que o eixo x é a abscissa e o eixo y é a ordenada. Veja:

FUNÇÃO RAIZ

A função raiz é definida pela fórmula:

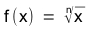
f(x) = imagem
x = domínio
n = índice

Podemos reescrever da seguinte forma:

f(x) = x1/n

• f(x) = imagem;

• 1/n = expoente. O n sempre deve ser positivo, ou seja, um número natural;

• x = domínio. O x pode ser positivo ou negativo. Para x positivo, n pode ser ímpar ou par; para x seja negativo, n poderá ser somente ímpar. Essa restrição está relacionada com o fato de não existir raiz quadrada para n par e x negativo.

GRÁFICO DA FUNÇÃO RAIZ

A função raiz é positiva e crescente. À medida que o valor numérico de n aumenta, o crescimento diminui. Veja um comparativo:

Para f(x) = x ½ (n = 2) e f(x) = x 1/5 (n = 5):

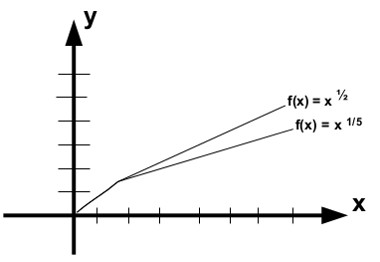
EXEMPLOS DE FUNÇÃO RAIZ

1) Resolva as funções. Considere x = 16.

a) f(x) = x ½

b) f(x) = x1/4

Solução

a) f(x) = x ½

f(x) = 161/2

Fatore:

16|2
08|2
04|2
02|2
01|

f(x) = (2)4 . ½

f(x) = (2)4/2

f(x) = (2)2

f(x) = 4

b) f(x) = x1/4

f(x) = 161/4

Utilize a fatoração obtida anteriormente:

f(x) = 24 . ¼

f(x) = 24/4

f(x) = 21

f(x) = 2

Link:https://mundoeducacao.uol.com.br/matematica/funcao-raiz.htm

Acessado em 27/11/2021

Comentário: sabemos que a função raiz é real e positiva para qualquer valor de X porque sabemos que  X pertence ao conjunto dos números naturais logo a função raiz exige uma fatoração e pode ser utilizada por exemplo para determinação de áreas para fins geométricos.

Função modular

MATEMÁTICA

Dada uma função, ela pode ser modular quando ela é uma função f: A → B, cuja lei de formação possui, pelo menos, uma variável dentro do módulo.

Gráfico de uma função modular

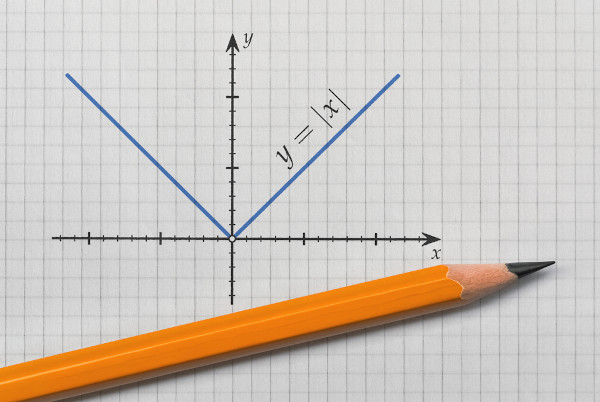
Função modular é a função f: A→ B, em que a lei de formação contém, pelo menos, uma variável dentro do módulo. O módulo ou valor absoluto de um número é representado por |n|, que gera como resultado o valor absoluto, ou seja, um número real positivo.

Existem diferentes tipos de funções modulares, a depender do tipo de equação que se encontra dentro do módulo, podendo ser uma equação do 1º grau, do 2º grau, entre outros tipos de expressões algébricas. Encontramos o valor numérico de uma função quando substituímos a variável pelo valor desejado, então o valor numérico da função quando x = k é igual a f(k). Durante o estudo da função, a representação gráfica também é muito importante para analisarmos o comportamento da variável.

Resumo sobre função modular

• Uma função é modular quando existir uma variável dentro do módulo em sua lei de formação.
• O valor numérico da função é encontrado quando substituímos x pelo valor desejado.
• A função modular pode ter em seu módulo qualquer tipo de equação, como uma equação de 1º ou 2º grau.

O que é uma função modular?

Classificamos uma função como modular quando essa função for f : A → B e, em sua lei de formação, existir uma variável que esteja dentro do módulo.

Exemplos:

• f(x) = |x|
• f(x) = |x² – 3x + 5|
• h(x) = |sen (x)|
• i(x) = |2x + 1| – 4

Para compreender o que é uma função modular, é importante lembrarmos o que é o módulo de um número. O módulo de número n por |n|, por definição, é:

Vejamos alguns exemplos a seguir:

• |4| → Sabemos que 4 > 0 → |4| = 4
• |-3| → Sabemos que -3 < 0 → |-3| = – (-3) = 3

Note que o módulo de um número é sempre o seu valor absoluto, ou seja, sempre positivo.

|-2,4| = 2,4

|1000| = 1000

Acessado em 27/11/2021 

Link: https://brasilescola.uol.com.br/matematica/funcao-modular.htm

comentário : Na função modular não temos resultado de  f(x) = |x| com valor negativo e na representação cartesiana vai ter sempre seu gráfico espelhado para parte positiva. 

aplicação de função de segundo grau na física

 

Aplicações da Função do 2º grau na Física

A função do 2º grau está presente em inúmeras situações cotidianas, na Física ela possui um papel importante na análise dos movimentos uniformemente variados (MUV), pois em razão da aceleração, os corpos variam a velocidade e o espaço em função do tempo.

Uma função do 2º grau obedece à seguinte lei de formação f(x) = ax2 + bx + c,
na Física a expressão que relaciona o espaço em função do tempo é dada pela expressão S = S0 + V0t + (at2)/2, onde    
a: aceleração, S: espaço, V: velocidade e t: tempo.

Exemplo 1

Um móvel realiza um MUV obedecendo à função S = 2t2 - 18t + 36, sendo s medido em metros e t em segundos. Em que instante o móvel muda de sentido?

Resolução:
A equação do movimento é do segundo grau, então ela descreve uma parábola crescente (a > 0), a mudança de sentido do móvel dará no momento em que ele atingir o ponto mínimo da parábola. Observe a ilustração do movimento do móvel:

Devemos calcular o ponto mínimo da parábola, dado por:


Exemplo 2

Um canhão atira um projétil (figura), descrevendo a função s = -9t2 + 120t, sendo s em metros e t em segundos. Calcule o ponto máximo de altura atingida pelo projétil.





Resolução:
A função do movimento do projétil descreve uma parábola decrescente (a < 0), o ponto máximo da parábola será a altura máxima atingida pelo projétil.

link:https://mundoeducacao.uol.com.br/matematica/aplicacoes-funcao-2-grau-na-fisica.htm

acessado em 27/11/2021

comentário:  vendo esse exemplo temos dimensão sobre a importância da função de segundo grau nas leis da física, onde podemos além de calcular a trajetória do movimento uniformemente variado, também  estabelecer os pontos dessa trajetória e fazer uma análise minuciosa do movimento da cinemática. 

utilização de função do primeiro grau

 

Link: https://sme.goiania.go.gov.br/conexaoescola/ensino_fundamental/utilizacao-da-equacao-do-primeiro-grau-no-cotidiano/

acessado em 27/11/2021 

Comentário: sabendo dessas aplicabilidades da função de primeiro grau  podemos por exemplo definir uma equação de primeiro grau para calcular  o lucro de uma empresa: sabendo que o lucro se define por (receitas- custo ) podemos dizer que L(x)= R(x)-c(x) 

Se uma mercadoria tem custo fixo de 100 reais dentre frete e produção + 20 de impostos  sendo 150 o valor de venda como podemos definir o lucro? sabendo que x é o numero de peças produzidas 

C(x) = 100 (custo fixo)+20x(custo variável) 

R(x)=150x

L=150x-(100+20x)=

L=130x-100

temos assim uma equação de lucro formada por uma função de primeiro grau que é usada no cotidiano.

 

Função exponencial

A função exponencial é utilizada para descrever e modelar o comportamento de várias situações no nosso dia a dia. Podemos observá-la, por exemplo, na matemática financeira, em situações que envolvem juros compostos, em reprodução de cultura de bactérias, e até mesmo o comportamento de novos casos da covid-19, durante a pandemia em 2020, aproxima-se muito de um comportamento exponencial.

A lei de formação da função exponencial é f(x) = ax, podendo gerar um gráfico crescente ou decrescente, dependo do valor da base “a”. A função inversa da função exponencial é a função logarítmica.

Definição da função exponencial

Definimos como função exponencial uma função f: ℝ → ℝ*+, ou seja, seu domínio é o conjunto dos números reais, e seu contradomínio é o conjunto dos números reais positivos diferentes de 0. Além disso, a sua lei de formação pode ser descrita por f (x) = ax, em que ‘a’ é a base, cujo valor sempre será um número real positivo.

Exemplos:

f(x) = 2x

f(x) = 0,3x

Podemos observar que f(x) é a variável dependente, podendo ser representada por y também, e x é a variável independente.

Tipos de função exponencial

Podemos dividir a função exponencial em dois casos: crescente ou decrescente.

O gráfico da função f(x) = ax é crescente quando a base é um número maior do que 1, ou seja, quando a > 1. Nesse caso, quanto maior o valor de x maior será o valor de y.

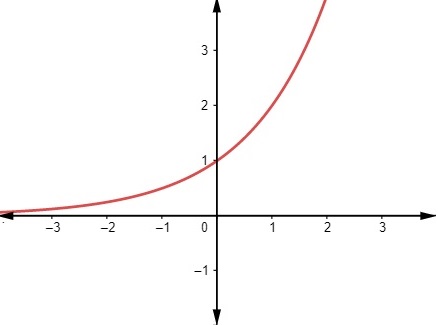
A função exponencial é decrescente quando a base é um número maior que 0 e menor que 1, ou seja, quando 0<a<1. Caso ela seja decrescente, quanto maior o valor de x menor será o valor de y.

Gráfico da função exponencial

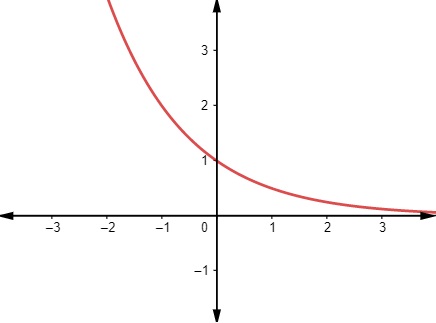
Para traçar o gráfico de uma função exponencial, é necessário encontrar o valor numérico para alguns valores de x. Existem duas possibilidades para o comportamento do gráfico, ele pode ser crescente ou decrescente, como vimos anteriormente. Quando o gráfico é crescente, a função exponencial é caracterizada por possuir um crescimento muito rápido em comparação, por exemplo, com a função afim.

Podemos observar que o gráfico não passa pelo 3º e 4º quadrante do plano cartesiano, pois o contradomínio será, como vimos na definição, os reais positivos e maiores que 0. Por mais próximo que o gráfico chegue do eixo x, ele não o tocará, não há valor algum no domínio que faça com que ax seja igual a 0, lembrando que, por definição, a base é sempre maior do que 0.

Propriedades da função exponencial

• 1ª propriedade

Em uma função exponencial, f(0) = 1. Essa propriedade não passa de uma consequência das propriedades de potência, já que a base de todo número diferente de 0 elevado a 0 é igual a 1.

f(0) = a0=1

• 2ª propriedade

A função exponencial é injetiva. Isso significa que, para valores diferentes de x, a imagem também será diferente, ou seja, f(x1) ≠ f(x2) com x1 ≠ x2. Ser injetiva significa que, para valores diferentes de y, existirá um único valor de x que faz com que f(x) seja igual a y.

• 3ª propriedade

Como vimos em um tópico anterior, o gráfico da função exponencial pode ser crescente, se a base for maior que 1 (a >1), e decrescente, caso a base seja um número menor que 1 e maior que 0 (0<a<1).

• 4ª propriedade

O gráfico da função exponencial nunca corta o eixo x. Por menor que seja o valor da imagem, ele nunca chegará a ser 0. Dizemos que ele tende a 0, mas não existe valor de x que faça com que f(x) = 0.

Função exponencial e função logarítmica

A comparação entre essas duas funções é bastante comum, já que a função logarítmica possui como função inversa a função exponencial. Isso significa que os gráficos das duas são simétricos em relação à bissetriz do eixo x.

link:https://mundoeducacao.uol.com.br/matematica/funcao-exponencial.htm

Acessado em 27/11/2021 

comentário: as funções exponenciais são usadas  para calcular situações nas quais ocorrem uma altíssima taxa de variação como taxas de juros, taxas populacionais, contagem de bactérias, distâncias astronômicas etc...

 

Função bijetora

Quando dizemos que uma função é bijetora (também chamada de bijetiva ou bijeção), significa que a função é injetora  e sobrejetora  ao mesmo tempo. Vamos relembrar estes conceitos:

Função injetora e sobrejetora

Uma função f é definida como uma relação entre dois conjuntos quaisquer, A e B, e uma regra que permite associar a cada elemento de A um único elemento de B. Isto quer dizer, em linguagem matemática, que:

f : A → B

Lê-se: f de A em B.

Chamamos o conjunto A de Domínio da função e B o Contradomínio. É importante atentar-se à diferença entre função f, que é a própria função, e f(x) que é o valor da função em um determinado ponto x no seu domínio. Sendo assim, podemos dizer que para cada valor de x que pertence ao domínio A, existe um único valor y (ou f(x)) que pertença ao contradomínio B. Usualmente escrevemos:

y=f(x)↔{x∈A e y∈B}

Podemos representar uma função através de um diagrama, como no exemplo abaixo:

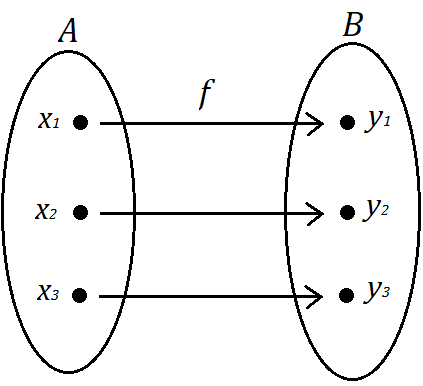
Também temos que uma função é chamada de injetora quando ela obedece estas condições:

(∀x1,x2∈A)x1≠x2⇒f(x1)≠f(x2)

Lê-se: Para quaisquer x₁, x₂ pertencentes ao conjunto A onde x₁ é diferente de x₂ então f(x₁) é diferente de f(x₂).

Uma função (ou aplicação) f : A → B é dita sobrejetora quando, para todo y∈B existe pelo menos um y∈B tal que f(x) = y. Em linguagem matemática escrevemos:

(∀y)y∈B⇒∃x∈A:f(x)=y

Lê-se: Para qualquer y, onde y pertence ao conjunto B, então existe x pertencente ao conjunto A tal que f(x) = y.

Função bijetora

Como dito anteriormente, uma função bijetora é tanto injetora quanto sobrejetora. Logo, as definições de injeção e sobrejeção valem para uma mesma função quando está é chamada de bijetora/bijetiva. Vejamos alguns exemplos:

Exemplo 1) Dada a aplicação f:R→R definida pela lei f(x)=3x+1, é bijetora, pois:

→ Dados x1,x2∈R então vale dizer que:

3x1+1≠3x2−1⇒f(x1)≠f(x2)

Então f é injetiva.

→ Dado y∈R então existe x∈R onde f(x) = y. Provando isto, temos:

3x+1=y⇒x=y−13

Note que para qualquer valor de y na igualdade acima existirá um valor real x que satisfaz a condição de sobrejeção.

Concluindo, a função f(x) = 3x+1 é bijetora.

Observação:

As funções não podem ser divididas em injetivas e sobrejetivas porque existem diversas aplicações que não são nem uma coisa nem outra. Um caso clássico é a função do tipo f:R→R definida por f(x)=x2 , onde ela não é nem sobrejetiva e nem injetiva. Veja:

2≠−2, porém f(2)=4=f(−2). Logo não é injetiva.

−1∈R , mas −1∉Im(f)=R+. Também não é sobrejetiva.

link: https://www.infoescola.com/matematica/funcao-bijetora/

acessado em 27/11/2021

comentário:  vemos que a função bijetora é quando a função é simultaneamente injetora e sobrejetora: ou seja  quando a imagem é igual ao contradomínio e ao mesmo tempo quando tiver elementos diferentes do domínio devem ter imagens diferentes.