Função modular
MATEMÁTICA
Dada uma função, ela pode ser modular quando ela é uma função f: A → B, cuja lei de formação possui, pelo menos, uma variável dentro do módulo.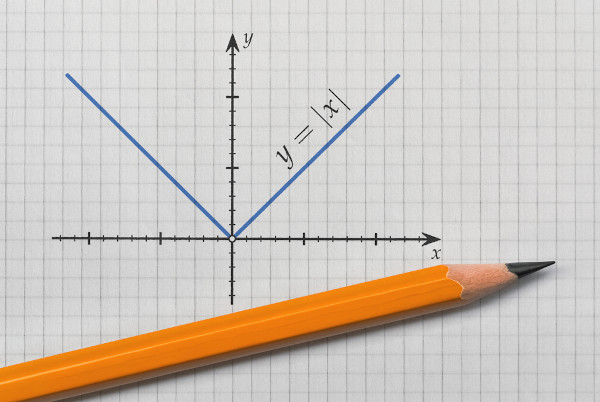
Função modular é a função f: A→ B, em que a lei de formação contém, pelo menos, uma variável dentro do módulo. O módulo ou valor absoluto de um número é representado por |n|, que gera como resultado o valor absoluto, ou seja, um número real positivo.
Existem diferentes tipos de funções modulares, a depender do tipo de equação que se encontra dentro do módulo, podendo ser uma equação do 1º grau, do 2º grau, entre outros tipos de expressões algébricas. Encontramos o valor numérico de uma função quando substituímos a variável pelo valor desejado, então o valor numérico da função quando x = k é igual a f(k). Durante o estudo da função, a representação gráfica também é muito importante para analisarmos o comportamento da variável.
Resumo sobre função modular
- Uma função é modular quando existir uma variável dentro do módulo em sua lei de formação.
- O valor numérico da função é encontrado quando substituímos x pelo valor desejado.
- A função modular pode ter em seu módulo qualquer tipo de equação, como uma equação de 1º ou 2º grau.
O que é uma função modular?
Classificamos uma função como modular quando essa função for f : A → B e, em sua lei de formação, existir uma variável que esteja dentro do módulo.
Exemplos:
- f(x) = |x|
- f(x) = |x² – 3x + 5|
- h(x) = |sen (x)|
- i(x) = |2x + 1| – 4
Para compreender o que é uma função modular, é importante lembrarmos o que é o módulo de um número. O módulo de número n por |n|, por definição, é:
![]()
Vejamos alguns exemplos a seguir:
- |4| → Sabemos que 4 > 0 → |4| = 4
- |-3| → Sabemos que -3 < 0 → |-3| = – (-3) = 3
Note que o módulo de um número é sempre o seu valor absoluto, ou seja, sempre positivo.
|-2,4| = 2,4
|1000| = 1000
Nenhum comentário:
Postar um comentário